Pictures tell a story way better than words. And in the language of nature which is mathematics, words are often too few. Finding easier ways to explain abstract math concepts can be very helpful. There are a lot of visual illustrations for math concepts or proofs, which range from simple to very abstract, that make the ideas easier to understand. Here are some I collected, mostly from elementary mathematics.

What is the circumference of a circle with a unit diameter? Well, you can use the well known equation $latex \pi*D $ and say it is $latex \pi$. Or you can take a look at this gif.

The sum of the exterior angles of any convex polygon will always add up to $latex 360^o$. You can try to prove that for a polygon with $latex n$ sides. The proof without words is shown here.

Angles can be measured in degrees or radians and most of us know how to convert one to the other. But what is a radian really? What does 1 rad mean, without looking at its equivalent in degrees? That is illustrated here.

Here is one way to prove Pythagoras’ theorem without writing a single equation. Simple but smart!

Onto a not so elementary one! There is a theorem that says the sum of the first $latex n$ odd numbers is equal to $latex n^2$. How would you prove that? Here is how. And that is way easier than this. Note that this one is not animated.

To explore more of these, just google ‘visual math proofs’ or ‘proofs without words’. There are also some books on this topic. Enjoy!

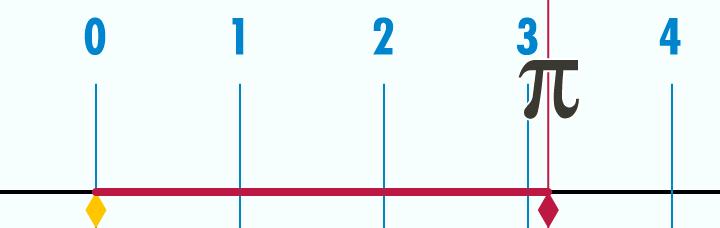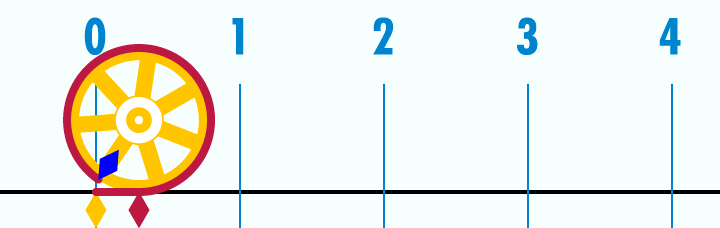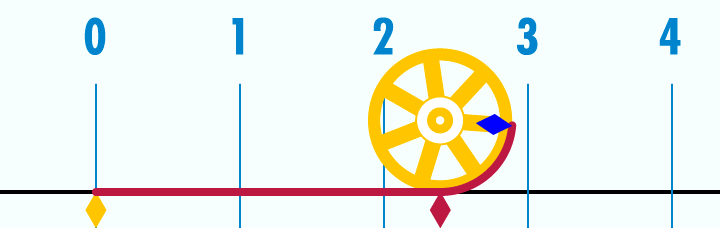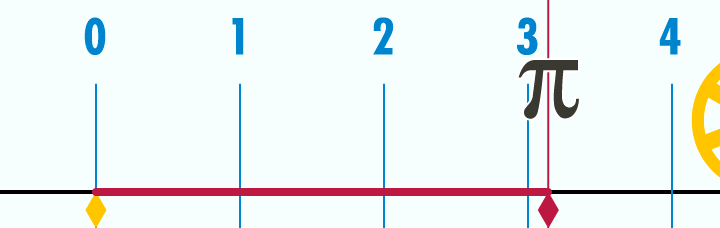
Credits:

http://math.stackexchange.com/questions/733754/visually-stunning-math-concepts-which-are-easy-to-explain
http://mathoverflow.net/questions/8846/proofs-without-words
http://math.berkeley.edu/~rbayer/09su-55/handouts/ProofByPicture-printable.pdf
http://en.wikipedia.org/wiki/Proof_without_words