There are several mathematical statements or problems that do not make sense at all at first glance, until closely scrutinized. A detailed examination then proves that the statements are true and shows that they are completely counterintuitive. Here are some of my favorite examples.

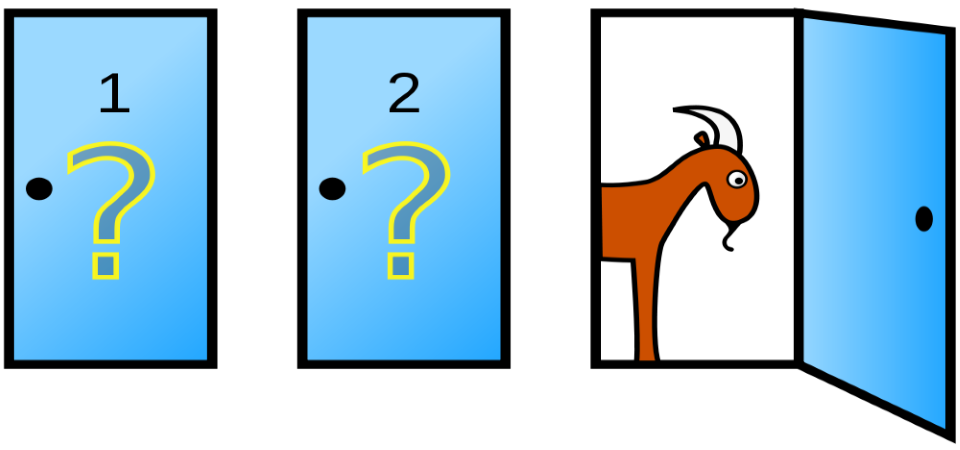
The Monty Hall problem

The Monty Hall problem is a puzzle where the underlying mathematical explanation is based on probability theory. A short statement of the problem reads:

There are three doors: A, B and C. There is a car behind one of them and goats behind the other two. You are given a chance to pick a door and win what is behind. You will pick one of the doors (say A) and then from the other two doors (B and C) the one which has a goat behind is revealed to you (say B). Now, you are told that you are free to switch your choice to the other remaining door i.e. C. Will you have a better chance of winning the car if you switch your choice from A to C or if you stay with your choice of A?

A quick and intuitive decision seems that it doesn’t make a difference if you stay with door A or switch to door C; your chance appears 50/50. But it is not! You always have a better chance of winning the car if you switch your choice. Here is a mathematical explanation:

Your initial chance of winning the car is 1/3. After a door which has a goat behind is revealed, if you stay with your choice, your chance of winning is still 1/3. But the other door suddenly holds the remaining 2/3 odds. So, switching gives you a 2/3 chance of winning. That still doesn’t seem to make sense, right? A detailed evaluation helps. There are three possible locations of the car.

1. A – car, B – goat, C – goat: You choose A. B is revealed to you. If you stay with A, you win. If you switch, you lose.
2. A – goat, B – car, C – goat: You choose A. C is revealed to you. If you stay with A, you lose. If you switch, you win.
3. A – goat, B – goat, C – car: You choose A. B is revealed to you. If you stay with A, you lose. If you switch, you win.

So, switching wins you the car 2/3 of the time! The concept works for any number of choices other than 3. Have a look at this video for more explanation.

The sum of all natural numbers

Natural numbers are ordinary numbers that we use for counting i.e. $latex 1,2,3…$. So, what is the sum of all natural numbers? An intuitive answer is positive infinity. The series is actually divergent and a trick used as a finite sum result is:

$latex 1+2+3+…=~-\frac{1}{12}$

What?! That’s impossible! Did you say that? Here is a mathematical proof by Srinivasa Ramanujan. Let’s call the sum $latex s$,

$latex s = 1 + 2 + 3 + 4 + 5 + 6 + …$,

multiply it by $latex 4$,

$latex 4s = 4 + 8 + 12 + …$,

and then take the difference between the two (we subtract even numbers from even numbers and keep the odd ones) to get

$latex -3s = 1 – 2 + 3 – 4 + 5 – 6 + …$

But $latex 1 – 2 + 3 – 4 + 5 – 6 + …$ is a well-known alternating series which converges to $latex 1/4$. Thus, we have:

$latex -3s = \frac{1}{4} \Rightarrow s = -\frac{1}{12}$

Things get a bit spooky when infinities are involved. This sum has, surprisingly, found an application in theoretical physics, particularly in string theory.

Benford’s law

If you are given a set of numerical data about some naturally occurring item or event (e.g. depths of lakes), how many of the numbers would you guess have 1 as a first digit? How many with 2? There are 9 possibilities. It appears that all numbers from 1 to 9 have the same chance of being the first digit. That’s not usually the case, though. Frank Benford has worked out a distribution that is almost always true for numbers in nature or related to nature. He stated that the number ‘1’ appears as the first digit about 30% of the time, ‘2’ about 17% of the time and decreasing for the next digits, with ‘9’ having the least chance of about 5%. This law is actually used to detect fraud in financial markets. Checkout this video.